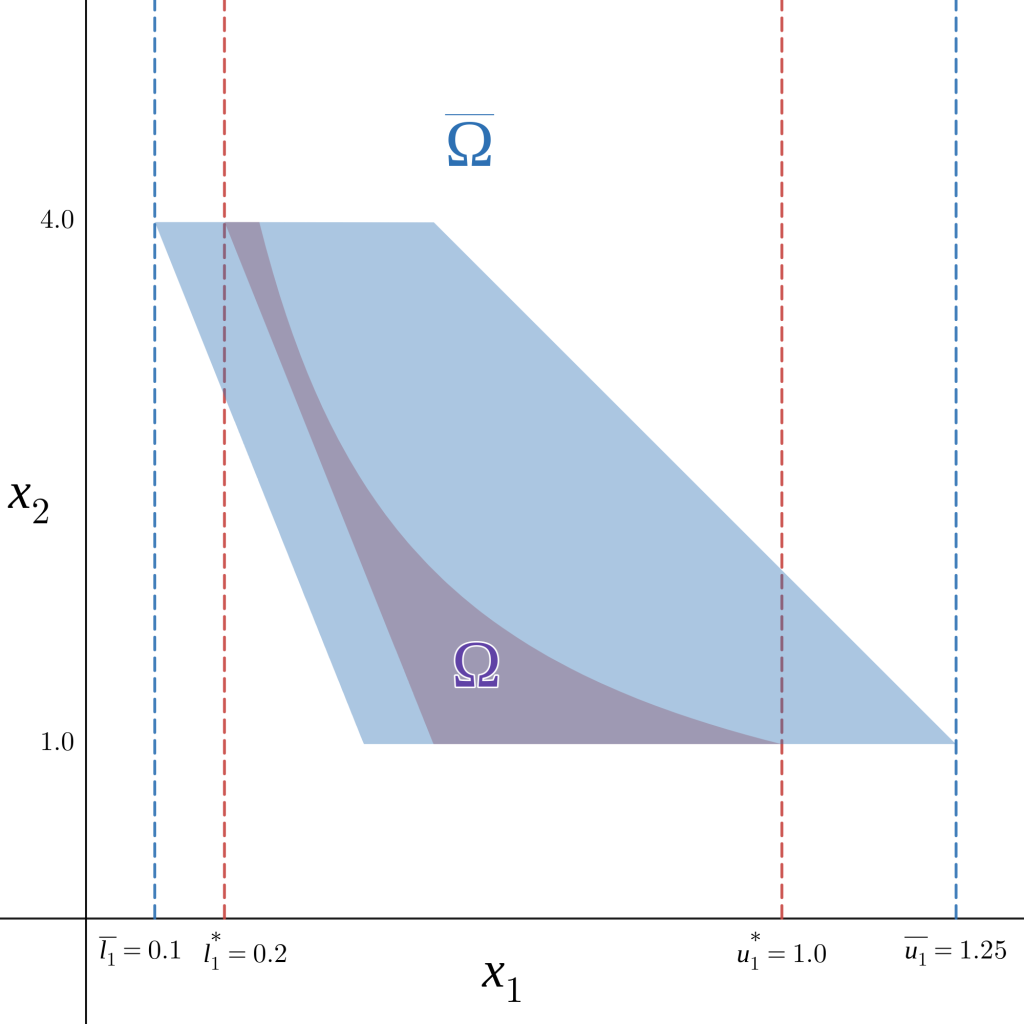
Coming back to our initial example (problem (P)), instead of trying to find the tightest bounds \(l_1^\star\) and \(u_1^\star\) over the set \(\Omega = {(x_1,x_2): x_1x_2 \leq 1, -10x_1-x_2\leq-6, 0 \leq x_1 \leq 1.5, 1\leq x_2 \leq 4}\), consider the set \(\overline{\Omega} = {(x_1,x_2): -10x_1-x_2\leq-5, 4x_1+x_2 \leq 6,0 \leq x_1 \leq 1.5, 1\leq x_2 \leq 4} \subseteq \Omega\) (blue area in Figure 2).
Then the problems \(\displaystyle \overline{l_1}=\min_{x_1,x_2 \in \overline{\Omega}} \text{ }x_1\) and \(\displaystyle \overline{u_1}=\max_{x_1,x_2 \in \overline{\Omega}} \text{ }x_1\) are linear, easy to solve, and given that \(\overline{\Omega}\) is a relaxation of \(\Omega\), \(\overline{l_1}\) and \(\overline{u_1}\) (0.1 and 1.25, in this case) are valid tighter bounds for the variable \(x_1\) (blue dashed lines in Figure 2) compared to the original bounds 0 and 4.
OBBT then finds under and over estimators \(\overline{l_i}\) and \(\overline{u_i}\) of \(l_i^\star\) and \(u_i^\star\) by relaxing the original feasible set. The better the relaxation, the closer the estimators would be from the tightest bounds.
Putting this into practice
In general, for each variable \(x_i \in [l_i, u_i]\) the following problems are solved using a relaxation \(\overline{\Omega}\) of \(\Omega\):
\(\overline{l_i}=\min_{{x}\in\overline{\Omega}}x_i\) and \(\overline{u_i}=\max_{{x}\in\overline{\Omega}}x_i\). If \(\overline{l_i}>l_i\) then the lower bound is set now to \(\overline{l_i}\) and if \(\overline{u_i}< u_i\) then the upper bound is set now to \(\overline{u_i}\).
If any of the problems is found to be infeasible, then it can be concluded that the original problem is infeasible too.
For a problem with \(n\) variables, one iteration of OBBT corresponds to solving \(2n\) optimisation problems, which makes OBBT an expensive method. Of course, after one iteration of OBBT is applied and the bounds are updated (assuming the problem was not found infeasible), the process can be repeated using the same relaxation with the (possibly) tighter bounds.
Octeract Engine uses OBBT on linear relaxations. In this case, \(\overline{\Omega}\) corresponds to a polytope, and given that the objective function of the new problems is just a linear term, the resulting problem used to tighten the bounds of the variable \(x_i\) is a linear problem too.
